今天看到了一篇文章《Mix-LN: Unleashing the Power of Deeper Layers by Combining Pre-LN and Post-LN》，分析了在大模型中，Post或Pre的Normalize方式对模型训练的影响。十分简单的分析，但是十分有启发性。

Pre or Post Normalize

对于一个残差块，输入为 $x$ ，输出为 $y$ 。目前大模型基本采用了两种的Normalize方式，分别为Pre-Norm：

$y_{pre} = x + \mathcal{F}(\textit{LN}(x)),$

和Post-Norm：

$y_{post} = \textit{LN}(x + \mathcal{F}(x)).$

其中 $\mathcal{F}$ 为残差块中的前馈网络， $\textit{LN}$ 为Layer Normalization。

对于LN：

$\textit{LN}(x) = \frac{x - \mu}{\sqrt{\sigma^2 + \epsilon}} \cdot \gamma + \beta.$

为了简化分析，我们忽略掉LN可学习的尺度和偏移参数，并且假设输入 $x$ 的分布是固定的（即 $\mu$ 和 $\sigma$ 是常数），对LN求导：

$\frac{\partial \textit{LN}}{\partial x} = \frac{1}{\sqrt{\sigma^2 + \epsilon}}.$

对两种方法求导：

$\frac{\partial y_{pre}}{\partial x} = 1 + \frac{\partial \mathcal{F}}{\partial \textit{LN}} \cdot \frac{\partial \textit{LN}}{\partial x} = 1 + \frac{\partial \mathcal{F}}{\partial \textit{LN}} \cdot \frac{1}{\sqrt{\sigma^2 + \epsilon}}.$

$\frac{\partial y_{post}}{\partial x} = \frac{\partial \textit{LN}}{\partial (x + \mathcal{F}(x))} \cdot \frac{\partial (x + \mathcal{F}(x))}{\partial x} = \frac{\partial \textit{LN}}{\partial (x + \mathcal{F}(x))} \cdot (1 + \frac{\partial \mathcal{F}}{\partial x}) = \frac{1}{\sqrt{\sigma^2 + \epsilon}} \cdot (1 + \frac{\partial \mathcal{F}}{\partial x}).$

在实际训练中，我们会观察到 $\sigma$ 的值会随着训练的进行而逐渐变大，这会导致什么结果呢？

对于 $\frac{\partial y_{pre}}{\partial x}$ 而言， $\frac{1}{\sqrt{\sigma^2 + \epsilon}}$ 会逐渐变小，导致 $\frac{\partial y_{pre}}{\partial x} = 1$ 。一般而言，深层的 $\sigma$ 会远大于浅层，因此在深层的残差块会失去意义。

对于 $\frac{\partial y_{post}}{\partial x}$ 而言， $\sigma$ 指的是 $x + \mathcal{F}(x)$ 的标准差。 $\frac{1}{\sigma^2 + \epsilon} < 1$ ，随着梯度的回传，浅层的梯度会消失。

实验观察

基于上面的分析，原论文中对于在不同Normalize方式下训练的大模型进行了“删层”实验，即在训练过程中，删除一些层，观察模型的性能变化。

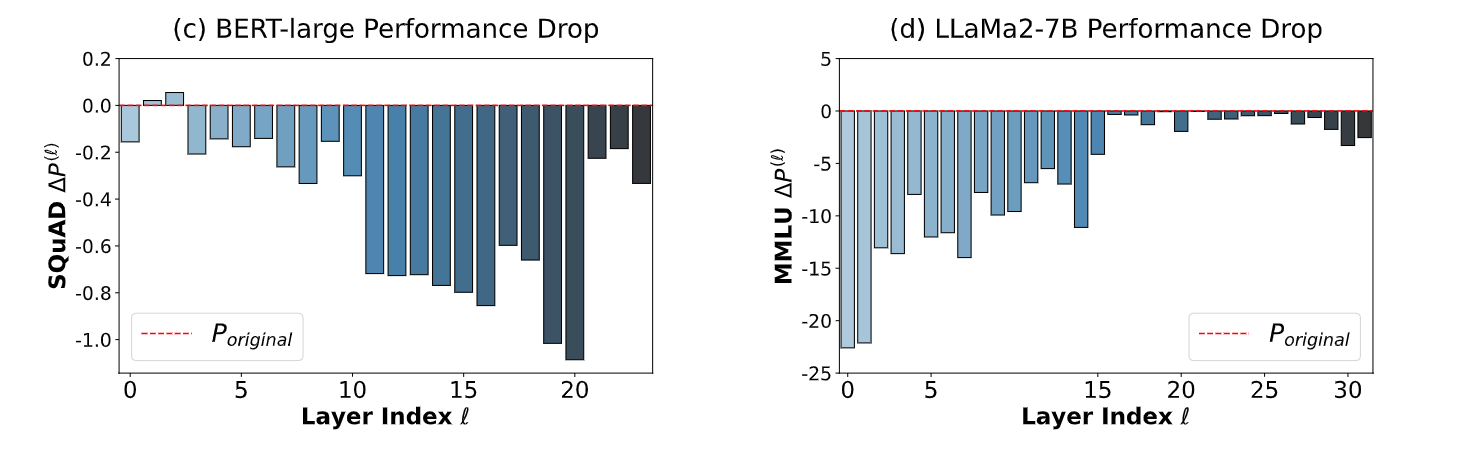
BERT采用的是Post-Norm，而LLama-2采用的是Pre-Norm。由图可以发现，Post-Norm在删除浅层块后，性能变化不明显，说明浅层块对模型影响不大。相反，Pre-Norm在删除浅层块后，性能变化明显，说明浅层块对模型影响很大。